| Wed March 4th 2015 16:00 – 17:00 ZH286 | Seminar | Transport and mixing properties in bubbly flows Elise Alméras |
Details:Transport and mixing properties in bubbly flowsE. Alméras1,2, F. Risso1, V. Roig1, C. Plais2, F. Augier2 1 IMFT, Université de Toulouse & CNRS, allée du Professeur Soula, 31 400 Toulouse, France 2 IFP Energies nouvelles, Rond-point de l’échangeur de Solaize, BP 3, 69360 Solaize, France Bubble columns are commonly used for chemical processes because of their good mixing capabilities. The development of physical models is necessary to improve the designs of bubble columns. The purpose of this work is to review mixing and scalar transport equations in a bubbly flow by distinguishing the contribution of the pseudo-turbulence induced by bubbles from that of shear-induced turbulence. That’s why the dispersion of a low diffusive scalar has been investigated in various experimental configurations. In each case, a specific technique has been developed to measure the concentration of the scalar. The first configuration is a bubbly flow in a Hele-Shaw cell where the confinement prevents from the development of turbulence. In this case, mixing is controlled by the capture and the transport by the bubble wakes (Figure a). This mechanism, which cannot be described by an effective diffusivity, has been modeled by considering the intermittent transport of finite volumes of dye. The second configuration is a homogeneous swarm of rising bubbles where the mixing results from the dispersion by the bubble-induced turbulence (Figure b). In this condition, the mixing can therefore be modeled by an anistropic effective diffusivity, which has been measured for gas volume fractions from 1 to 15%. The effective diffusivity can be written as the product of the variance of the velocity fluctuations by a characteristic diffusion time, which depends on the gas volume fraction. At low gas volume fraction, it is estimated from the integral Lagrangian length scale whereas it is limited by the average time between two bubble passages above a specific threshold. The last studied configuration is an inhomogenous bubbly flow, in which a mean liquid recirculation loop is present. In the case of a moderate inhomogeneity, shear induced-turbulence is not generated by the gradients of the mean flow and the mixing can be modelled by the sum of the bubble-induced dispersion and the advection by the mean flow (Figure c). Figure : (a) Mixing in a confined bubbly flow ; (b) Mixing in a homogeneous bubble colomn ; (c) Mixing in a inhomogeneous bubble colomn. 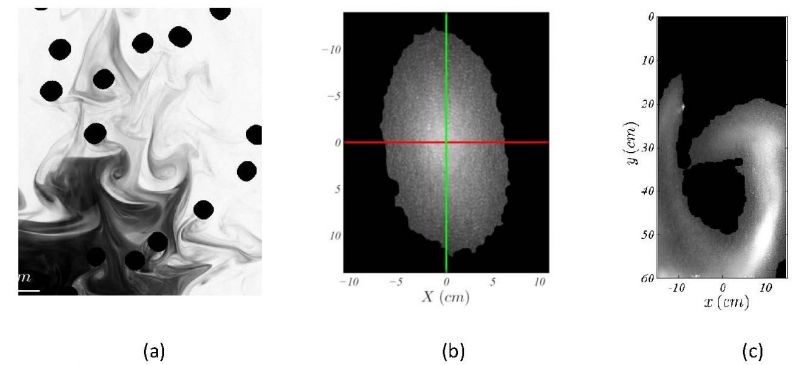 | ||